The Radiometric Foundation of Integrating Sphere Theory

Integrating spheres are fundamental instruments in the field of optical metrology, serving as the cornerstone for precise and accurate measurement of luminous flux, spectral power distribution, and other key photometric and radiometric quantities. Their operation is predicated on the principle of spatial integration, transforming a complex, spatially dependent light source into a uniform radiance field measurable at a single point. This spatial averaging is critical for applications where the angular distribution of radiation from a source is either unknown, highly variable, or simply too complex to characterize with goniometric methods. The theoretical underpinning of an integrating sphere is a near-perfect Lambertian diffuser with a highly reflective and spectrally flat interior coating. Incident light undergoes multiple diffuse reflections, and at each reflection event, the radiance is scattered in a cosine distribution, ensuring that the subsequent reflections contribute equally to all points on the sphere’s inner wall. This multiplicative process leads to a homogeneous distribution of light, where the radiance at any point on the sphere wall becomes proportional to the total flux introduced by the source.

The mathematical derivation of this principle begins with the fundamental integrating sphere equation. The spatially averaged radiance, L, at the sphere wall resulting from an input flux, Φ, is given by:

L = ( Φ • ρ ) / ( π • A • (1 – ρ (1 – f )) )

Where:
ρ is the average reflectance of the sphere wall,
A is the internal surface area of the sphere,
f is the port fraction, the ratio of the total area of all ports (including the detector port) to the total internal surface area.

This equation highlights the critical parameters governing sphere performance: wall reflectance and port fraction. A high wall reflectance (ρ → 1) is paramount for achieving high efficiency, as it minimizes the attenuation of light with each reflection. A low port fraction (f → 0) is equally crucial, as any open port represents a loss mechanism where light escapes without contributing to the integrated signal. Practical spheres achieve reflectances of 0.97 to 0.99 in the visible spectrum using materials such as sintered Polytetrafluoroethylene (PTFE) or specialized barium sulfate-based coatings, which exhibit excellent diffuse reflectance and near-Lambertian behavior.

Critical Design Parameters and Configurations for Measurement Accuracy

The practical implementation of integrating sphere theory requires meticulous attention to design parameters that can introduce significant measurement uncertainties if not properly managed. Beyond the basic wall reflectance and port fraction, the placement of baffles is a critical design element. A baffle is an opaque shield coated with the same diffuse material as the sphere wall, strategically positioned between the light source under test and the detector port. Its sole purpose is to prevent the first reflection of light from the source from directly entering the detector, which would violate the condition of spatial integration and lead to a measurement bias dependent on the source’s original spatial distribution. The baffle must be sized and placed to ensure that the detector has no direct line-of-sight to the source or to any port that could allow a direct path.

The selection of a sphere’s internal diameter is a compromise between measurement requirements and physical practicality. Larger spheres are generally preferred as they reduce the port fraction for a given set of auxiliary ports (e.g., for source power, external shuttering, or spectrometer input) and minimize the impact of spatial non-uniformities caused by the source itself and any internal obstructions like lamp holders. However, larger spheres require more powerful light sources to achieve a measurable signal level at the detector. The configuration of the sphere is also application-dependent. The most common is the 4π geometry, where the source is placed entirely inside the sphere for total luminous flux measurement. Conversely, a 2π geometry is used for measuring radiant flux from directional sources like LEDs or laser diodes, where the source is mounted on a port on the sphere’s exterior, emitting light inward.

System Calibration and the Role of Standard Lamps

The absolute accuracy of an integrating sphere system is contingent upon a rigorous calibration process traceable to national metrology institutes. This process typically employs a standard lamp, a light source with a known and stable spectral power distribution and total luminous flux output calibrated under strict conditions. The calibration procedure involves substituting the standard lamp for the device under test. The sphere system measures the signal generated by the standard lamp, and a calibration coefficient is computed, relating the measured electrical signal from the detector to the known photometric or radiometric quantity. This coefficient accounts for the sphere’s specific efficiency, spectral responsivity of the detector, and any other system-level gains.

This method, however, introduces an inherent systematic error known as the self-absorption effect or spatial flux alteration error. When a light source is placed inside the sphere, it physically occupies space and absorbs a portion of the internally reflected light that would otherwise contribute to the measured signal. The standard lamp and the device under test (DUT) are rarely identical in physical size, shape, and surface reflectance. Therefore, the amount of light each source absorbs from the sphere’s integrated field is different. This leads to a measurement error where the calibration factor derived from the standard lamp is not perfectly applicable to the DUT. Advanced systems mitigate this error through computational correction methods based on the auxiliary sphere technique or by using specially designed standard lamps that physically mimic the DUT.

The LPCE-3 System: Architecture for Precision Photometry

The LISUN LPCE-3 Integrating Sphere Spectroradiometer System exemplifies the application of these fundamental principles in a high-precision commercial instrument. Designed for the comprehensive testing of single LEDs and LED lighting products, the system integrates a precision-machined sphere with a high-reflectance coating, a CCD array-based spectroradiometer, and a software suite that automates calibration, measurement, and data analysis in compliance with CIE 177, CIE-13.3, IES LM-79-19, and ANSI C78.377 standards.

The core of the LPCE-3 system is its integrating sphere, available in multiple diameters (e.g., 0.3m, 0.5m, 1m, 1.5m, 2m) to accommodate different source sizes and flux levels. The interior is coated with a proprietary diffuse reflective material (MI-R6) offering a reflectance of >97% across the 380nm-780nm wavelength range, ensuring high efficiency and excellent spatial integration. A strategically placed baffle, coated with the same material, prevents direct illumination of the detector port. The system employs a 4π configuration for testing lamps and luminaries and a 2π configuration for testing individual LED modules. The light collected by the sphere is coupled via a fiber optic cable to the high-resolution CCD spectroradiometer, which captures the full spectral power distribution (SPD) of the source.

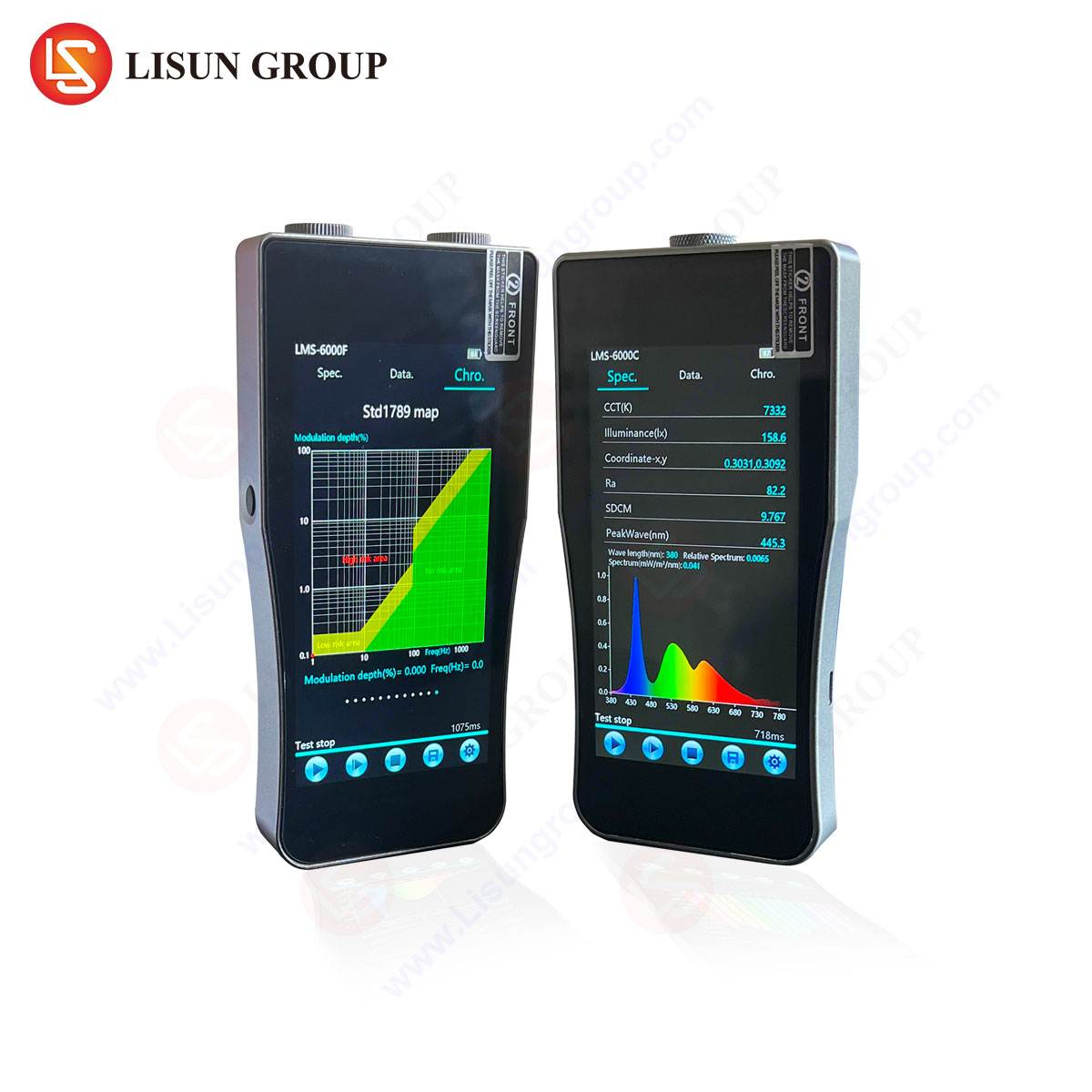
The system’s software is integral to its operation, automating the critical calibration sequence using a user-provided standard lamp. It applies advanced algorithms to correct for self-absorption error based on the specific geometries of the standard and the DUT. The output provides not only the total luminous flux but a complete photometric and colorimetric analysis, including chromaticity coordinates (CIE 1931, CIE 1976), correlated color temperature (CCT), color rendering index (CRI), peak wavelength, dominant wavelength, spectral purity, and luminous efficacy.

Cross-Industry Metrology Applications and Compliance

The precision and versatility of systems like the LPCE-3 make them indispensable across a wide spectrum of industries where accurate light measurement is critical to performance, safety, and compliance.

In LED & OLED Manufacturing and the broader Lighting Industry, the system is used for quality control, binning LEDs based on flux and chromaticity, and verifying compliance with energy efficiency standards and product datasheets. Automotive Lighting Testing requires rigorous validation of headlamps, taillights, and interior LEDs for luminous intensity, color, and conformity to regulations such as ECE and SAE. Similarly, Aerospace and Aviation Lighting and Marine and Navigation Lighting demand absolute reliability, with lights tested to ensure they meet specific chromaticity and intensity requirements for signal recognition and safety.

In Display Equipment Testing, the sphere measures the absolute luminance and color uniformity of displays and backlight units. The Photovoltaic Industry utilizes similar spheres with different coatings for measuring the spectral responsivity of solar cells. Optical Instrument R&D and Scientific Research Laboratories rely on these systems to characterize lasers, detectors, and other optical components. Urban Lighting Design projects use the data to select luminaires based on efficacy and color quality, while Stage and Studio Lighting and Medical Lighting Equipment manufacturers depend on accurate colorimetric data to ensure their products perform as intended for critical applications in entertainment and healthcare.

FAQ Section

Q1: How does the LPCE-3 system correct for the self-absorption error inherent in integrating sphere measurements?
The LPCE-3 system’s software incorporates algorithmic corrections for self-absorption error. The method typically involves calculating an absorption factor based on the physical dimensions and reflectivity of both the calibration standard and the device under test. By inputting these parameters, the software adjusts the final flux calculation, significantly reducing the systematic error that would occur if a simple substitution calibration were used without correction.

Q2: What are the advantages of using a CCD array spectroradiometer versus a photometer head in a system like the LPCE-3?
A CCD array spectroradiometer captures the entire spectral power distribution (SPD) in a single measurement. This allows for the simultaneous calculation of all photometric (e.g., luminous flux) and colorimetric (e.g., CCT, CRI, chromaticity coordinates) parameters from the same data set, ensuring internal consistency. A photometer, which uses a filtered detector to approximate the human eye response (V(λ) function), can only measure photometric quantities and is susceptible to errors if the source spectrum differs significantly from the calibration source.

Q3: For testing a high-power LED automotive headlamp, what sphere size would be recommended and why?
A sphere with a diameter of 1.5 meters or larger is generally recommended for high-power automotive headlamps. This is due to the high luminous flux output of these units, which could cause detector saturation in a smaller sphere. Furthermore, a larger sphere minimizes the port fraction and reduces the thermal load and the impact of spatial non-uniformities caused by the large physical size and complex geometry of the headlamp assembly inside the sphere.

Q4: Can the LPCE-3 system be used to measure the flicker percentage of a light source?
Yes, provided the spectroradiometer component of the LPCE-3 system has a sufficiently high sampling rate. While a standard system is optimized for steady-state measurement, configurations with high-speed spectroradiometers can capture rapid changes in intensity over time. The accompanying software can then analyze this temporal data to calculate flicker percentage, flicker index, and other temporal light modulation parameters in accordance with relevant standards like IEEE PAR1789.

Q5: How often should the integrating sphere system be recalibrated using a standard lamp?
The recalibration frequency depends on usage intensity, environmental conditions, and required measurement uncertainty. For high-precision quality control labs, a monthly recalibration is common. For less critical applications, a quarterly or semi-annual schedule may suffice. It is also good practice to perform a recalibration after any significant change to the system configuration, such as changing the sphere’s internal lining or if the system is physically moved. The stability of the system should be verified regularly with a stable reference source.